Sample Problem Using the Improved New Increment Technique for Weibull Analysis of Life Test Data by Including Partial Activities of Suspended Items
| Specimen No. | Running Time | Status |
| 1 | 302 Hours | Failed |
| 2 | 450 Hours | Suspended |
| 3 | 740 Hours | Failed |
| 4 | 800 Hours | Suspended |
| 5 | 900 Hours | Suspended |
| 6 | 1,005 Hours | Failed |
| 7 | 1,300 Hours | Suspended |
| 8 | 1,410 Hours | Failed |
Table 1 - Data Obtained on Test Specimen
In any statistical prediction problem involving items being used by customers in the field, it is important to attach the correct percentile number to each case of a failure. The method of "suspended items", that is, treating unfailed items together with failed ones, is presented as one solution in this difficult problem of placing failures in correct order within a population. Once this has been done, the prediction problem can be solved in a straightforward manner. The prediction method employed in this Weibull program is based on such theory of "suspended items". It frequently happens that one or more specimens in a life test remain unfailed for some reason or other (too long a waiting time, failures of a type other than the type tested for, the need for immediate analysis before failing all the specimens allotted to a test, and so on).
To illustrated, suppose 8 specimens were put on test originally, and that at some point in time the data shown in Table 1 were obtained. This data set would present no special difficulty if all eight specimens failed. However there were 4 specimens still unfailed or suspended at various times. We realize that the number of items following the suspended set is really the number of fully active items in the interval between two failures where in the suspended set appears. See DRI's Reliability Workbook "New and Effective Methods in Statistical Reliability - Introduction to Reliability and Entropy" for detailed analysis.
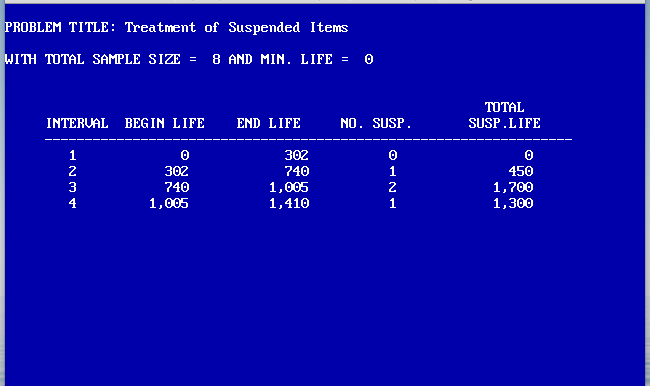
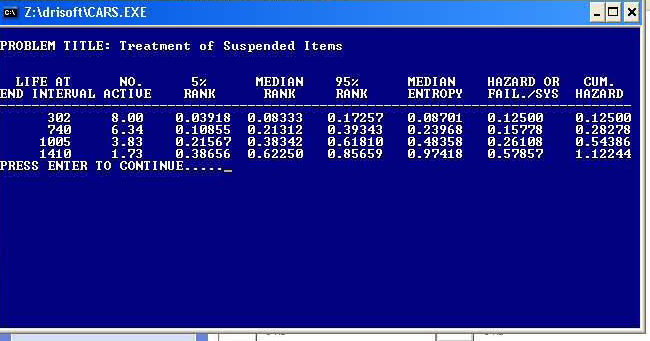
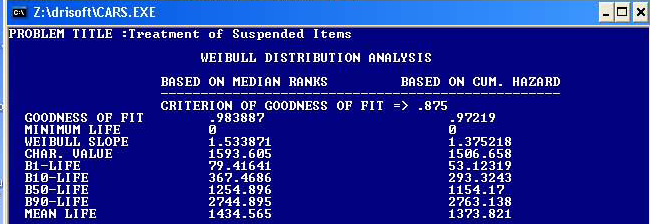
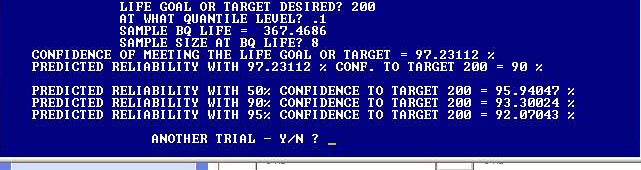
By including all partial activity contributed by the suspended items in a life testing data set, we have improved the accuracy of Weibull parameter determination by least square statistical approach using the Median Ranks of actual failures as determined by the new increments obtained from including partial activities of suspended items in each interval between successive failures. This is a clear illustration of how a theoretical approach becomes improved by including new factors, such as partial activities, which were formerly ignored in the statistical calculations. This is the way in which any theoretical science evolves with passage of time as man becomes more knowledgeable and sophisticated.
Download "WEIBULL" program to solve this example and see the difference between this Improved New Increment Technique and the standard new increment technique or other Weibull Analysis such as Maximum Likelihood approach.